Statistical Analysis of Worldwide Suicide Rates and Demographics
Topic Background
Suicide has become a topic of interest in recent years and in general, either through increased attention or increased suicide attempts, the perception is that suicide is becoming more prevalent. Completed suicide attempts affect our world in innumerable ways including emotional, socioeconomic, and personal levels. I sought to further explore suicide data and trends, perhaps as a way to see if there were certain factors that are predictive of suicide rates. The dataset is a Suicide Rates Overview from 1985-2016 obtained from Kaggle.com.
The dataset can be found at: https://www.kaggle.com/russellyates88/suicide-rates-overview-1985-to-2016.
Per the website on Kaggle, this dataset was compiled using information from the United Nations Development Program, the World Bank, Suicide in the Twenty-First Century Dataset, and the World Health Organization website on suicide prevention, some of which are hosted on Kaggle elsewhere. The fact that the data has been collected from several different sources could imbue some erroneous data due to multiple data sources.
The variables included in the dataset are Country, Year, Sex, Age, Number of Suicides, Population, Suicide Rate, Country-Year Composite Key, HDI for that Year, GDP for Year, GDP Per Capita, and Generation (i.e. Baby Boomer, Millennial etc.). Since the age ranges in provided in the dataset correlate with the generation status, I do not intend to use this variable in my analysis. The HDI variable was almost all NA values so will be removed. Furthermore, the country-year variable is redundant and will be excluded from the analysis. One note of caution is that Germany and South Africa do not have suicide data going back as far as the other three countries. This will be evident on the graphs later.
Primary Research Questions
-
Does suicide rate vary significantly between the US and the United Kingdom, South Africa, Germany, and France for the age range in question?
-
What is the suicide rate trend over the last 39 years for the United States?
-
Is GDP associated with suicide rate in the US? If yes, how is GDP correlated with the suicide rate?
-
Is GDP associated with suicide rate in the other 4 countries?
-
In the US, is there a difference in suicide rate based on age?
-
Is there a difference between suicide rate and gender in the United States?
Basic R packages were loaded and data was read into a dataframe.
Initial Analysis of Dataset
The dataset was analyzed using R and general descriptive statistics computed. As above, the countries of interest were United States, United Kingdom, France, Germany, and South Africa. The dataset was initially analyzed by suicide rates by age bracket, sex, year, population, suicide rate, total country GDP, and GDP per Capita.
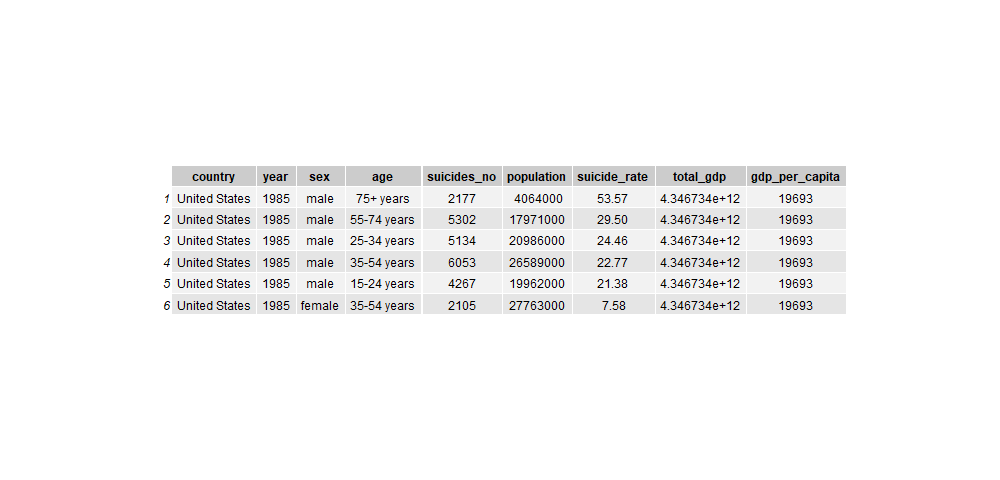
The years in the dataset range from 1985 to 2015. Each year is broken down into both male and female genders. The total number of suicides average was 1086 suicides with a mean suicide rate of 12.573. The mean GDP per Capita was $30268.
The data was then subset for ages 25-34 age range and split up with a male only dataframe and a female only dataframe for the five countries of interest.
For initial analysis, the data was separated into five different datasets based on our countries of interest. Histograms of suicide rate separated by gender were plotted for our five different countries are shown below.
ggplot(usdata, aes(x = suicide_rate, col = sex)) + geom_histogram(aes(y = ..density..), binwidth = 0.1) + stat_function(fun = dnorm, color = "red", args = list(mean = mean(usdata$suicide_rate, na.rm = TRUE), sd = sd(usdata$suicide_rate, na.rm = TRUE))) + xlab("Suicide Rate Per 100,000 People") + ylab("Counts") + ggtitle("Histogram for US Data on Suicide Rate")
ggplot(ukdata, aes(x = suicide_rate, col = sex)) + geom_histogram(aes(y = ..density..), binwidth = 0.1) + stat_function(fun = dnorm, color = "red", args = list(mean = mean(ukdata$suicide_rate, na.rm = TRUE), sd = sd(ukdata$suicide_rate, na.rm = TRUE))) + xlab("Suicide Rate Per 100,000 People") + ylab("Counts") + ggtitle("Histogram for UK Data on Suicide Rate")
ggplot(francedata, aes(x = suicide_rate, col = sex)) + geom_histogram(aes(y = ..density..), binwidth = 0.1) + stat_function(fun = dnorm, color = "red", args = list(mean = mean(francedata$suicide_rate, na.rm = TRUE), sd = sd(francedata$suicide_rate, na.rm = TRUE))) + xlab("Suicide Rate Per 100,000 People") + ylab("Counts") + ggtitle("Histogram for France Data on Suicide Rate")
ggplot(germanydata, aes(x = suicide_rate, col =sex)) + geom_histogram(aes(y = ..density..), binwidth = 0.1) + stat_function(fun = dnorm, color = "red", args = list(mean = mean(germanydata$suicide_rate, na.rm = TRUE), sd = sd(germanydata$suicide_rate, na.rm = TRUE))) + xlab("Suicide Rate Per 100,000 People") + ylab("Counts") + ggtitle("Histogram for Germany Data on Suicide Rate")
ggplot(safdata, aes(x = suicide_rate, col = sex)) + geom_histogram(aes(y = ..density..), binwidth = 0.1) + stat_function(fun = dnorm, color = "red", args = list(mean = mean(safdata$suicide_rate, na.rm = TRUE), sd = sd(safdata$suicide_rate, na.rm = TRUE))) + xlab("Suicide Rate Per 100,000 People") + ylab("Counts") + ggtitle("Histogram for South Africa Data on Suicide Rate")
.png)
.png)
.png)
.png)
.png)
There appears to be a significant contrast between male and female suicide rates per 100,000 people. South Africa’s difference between male and female suicide rates is less significant.
Initial Impressions:
Since our histograms appear non-normally distributed based on our histograms and have a small sample size since our data is a summary based on year and country, kendall correlation will be used to determine correlations between suicide rate and GDP per capita and country total GDP. While the GDP and GDP per capita may be very similar, I sought to analyze the relationship between GDP as an indicator of country wealth as opposed to the GDP per individual person.
The United States tends to have relatively flat association between GDP and suicide rate. For males, there actually were less suicides per 100,000 population between approximately 40-50,000 GDP per capita. Of these values computed, the only statistically significant correlations are between France’s suicide rate and gdp per capita, Germany’s suicide rate and gdp per capita, and between france and germany’s suicide rate and total gdp. These correlations are negative indicating that as GDP decreases (whether that be per capita or total), suicide rate tends to increase. The highest R^2 values of the correlation between the five countries appears to be France with R^2 of 0.1342 between suicide rate and GDP per capita and with an R^2 of 0.1359 between suicide rate and total GDP.
Interestingly enough, the South Africa correlations between suicide rate and GDP/GDP per capita suggests that as GDP per capita and Total GDP increase, the suicide rate increases.
Suicide Rates Plotted By Country and Gender
Next, the country’s suicide rates were plotted as line graphs and split up by gender.
ggplot(usdata, aes(x = year, y = suicide_rate, col = sex)) + geom_line() + geom_point() + ggtitle("Plot of US Suicide Rate by Year and Gender") + xlab("Year") + ylab("Suicide Rate per 100,000 People")
ggplot(ukdata, aes(x = year, y = suicide_rate, col = sex)) + geom_line() + geom_point() + ggtitle("Plot of United Kingdom Suicide Rate by Year and Gender") + xlab("Year") + ylab("Suicide Rate per 100,000 People")
ggplot(francedata, aes(x = year, y = suicide_rate, col = sex)) + geom_line() + geom_point() + ggtitle("Plot of France Suicide Rate by Year and Gender") + xlab("Year") + ylab("Suicide Rate per 100,000 People")
ggplot(germanydata, aes(x = year, y = suicide_rate, col = sex)) + geom_line() + geom_point() + ggtitle("Plot of Germany Suicide Rate by Year and Gender") + xlab("Year") + ylab("Suicide Rate per 100,000 People")
ggplot(safdata, aes(x = year, y = suicide_rate, col = sex)) + geom_line() + geom_point() + ggtitle("Plot of South Africa Suicide Rate by Year and Gender") + xlab("Year") + ylab("Suicide Rate per 100,000 People")
.png)
.png)
.png)
.png)
.png)
GDP Per Capita and Suicide Rates Separated By Country and Gender
Next, GDP per Capita and suicide rates were plotted by gender and separated by the five different countries.
ggplot(usdata, aes(x = gdp_per_capita, y = suicide_rate, col = sex)) + geom_line() + geom_point() + ggtitle("Plot of Suicide Rate Predicted By GDP Per Capita For US") + xlab("GDP Per Capita ($)") + ylab("Suicide Rate per 100,000 People")
ggplot(ukdata, aes(x = gdp_per_capita, y = suicide_rate, col = sex)) + geom_line() + geom_point() + ggtitle("Plot of Suicide Rate Predicted By GDP Per Capita For UK") + xlab("GDP Per Capita ($)") + ylab("Suicide Rate per 100,000 People")
ggplot(francedata, aes(x = gdp_per_capita, y = suicide_rate, col = sex)) + geom_line() + geom_point() + ggtitle("Plot of Suicide Rate Predicted By GDP Per Capita For France") + xlab("GDP Per Capita ($)") + ylab("Suicide Rate per 100,000 People")
ggplot(germanydata, aes(x = gdp_per_capita, y = suicide_rate, col = sex)) + geom_line() + geom_point() + ggtitle("Plot of Suicide Rate Predicted By GDP Per Capita For Germany") + xlab("GDP Per Capita ($)") + ylab("Suicide Rate per 100,000 People")
ggplot(safdata, aes(x = gdp_per_capita, y = suicide_rate, col = sex)) + geom_line() + geom_point() + ggtitle("Plot of Suicide Rate Predicted By GDP Per Capita For South Africa") + xlab("GDP Per Capita ($)") + ylab("Suicide Rate per 100,000 People")
.png)
.png)
.png)
.png)
.png)
Suicide Rates Separated By Gender and Plotted With All Five Countries Compared
Next, the data was between all five different countries for all males and then all females.
ggplot(countrymale, aes(x = year, y = suicide_rate, col = country)) + geom_line() + geom_point() + ggtitle("Plot of Five Different Country's Male Suicide Rate by Year") + xlab("Year") + ylab("Suicide Rate per 100,000 People")
ggplot(countryfemale, aes(x = year, y = suicide_rate, col = country)) + geom_line() + geom_point() + ggtitle("Plot of Five Different Country's Female Suicide Rate by Year") + xlab("Year") + ylab("Suicide Rate per 100,000 People")
.png)
.png)
For the male gender looking at suicide rates between the five different countries, this graph makes it suggests that suicide rates in France, UK, and Germany have a net downward trend with the France suicide rate decreasing the most. The US suicide rate initially declined and then has increased over recent years. The UK suicide rate for males increased in the 2000s and then has settled down to its suicide rate similar to what it was in the 1980s. The South Africa suicide rate for males also appears to be more or less stable. The US most recently has the highest current suicide rate followed by France, Germany, UK, and then South Africa.
For the female gender looking at suicide rates between the five different countries, this graph suggests that suicide rates for females have a downward trend for France and Germany. The South Africa and UK suicide rates appears approximately stable. However, of more concern is the rise in suicide rates in females in the US. Once again though, relatively speaking, the female suicide rates for all five countries are lower than the male suicide rate. While looking at South Africa though, the difference is quite small (on the order of 1-2 people per 100,000).
Since most of these graphs appear to show a linear relationship so we will start with a simple linear regression here and also do a multiple regression comparing suicide rate by country with the gdp per capita and gender.
Regression Analysis
Note: Full regression analysis information is in the GitHub repository under the R Markdown project documents.
Since the relationships on the above graphs appear linear, I started off with linear regression analyses and multiple regression and then checked for outliers and influential cases.
Using these models outlier and influential cases were examined. There were no statistically significant relationships between GDP and suicide rate for the US, UK, Germany, or South Africa. However, when adding in gender to our models, there was a statistically significant correlation between these variables with a high R^2 value. Furthermore, using a 95% confidence interval, none of the values crossed zero which is reassuring. The residual standard errors decreased for all five countries when added to the models. ANOVA between both models for each country showed that adding gender to the models significantly improved the fit of the model as compared to just GDP per capita.
Outlier Assessment and Influential Cases
.png)
An example of a Q-Q plot of the US suicide rates using linear regression with GDP per Capita and Gender predicting suicide rate is shown above.
Looking at the results, we have several large residuals for all five of our models comparing suicide rate with gender and total GDP. In none of them is the cook’s distance > 1 so it does not appear that they are having any undue influence on the model. While some of the leverage values and covariance ratios may be outside the range for our data set, since the Cook’s distance is <1, these are likely not significantly influencing the model.
However, the plots seemed to suggest that for our five different models, they violate the assumption of normality, especially in the tails where more extreme values are noted.
When the data was segmented into both male and female genders and compared across all five countries, the models illustrated a statistically significant relationship between country, gender, and GDP as predictors of the suicide rate. All of the residual standard errors are lower when adding in all of the other countries with the highest R^2 value being for the male dataset with a value of 0.913 compared with the R^2 of the female dataset with a value of 0.845.
Segmenting the Data Into Age Ranges for Each Country and Gender
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
The plots above have a significant amount of information. France, Germany, and the US male suicide rates have the highest suicide rates in the 75+ age category. For the UK male population, it is age 35-54 and for South Africa it is 75+ again.
Female suicide rates in the age 35-54 age range are highest in the US and UK. France and Germany’s female suicide rates are highest in the age 75+ age group. Finally South Africa’s suicide rates are highest in the 15-24 age group.
Finally, the data was segmented to the US for both males and females for age ranges of 25-34, total population, and GDP per capita.
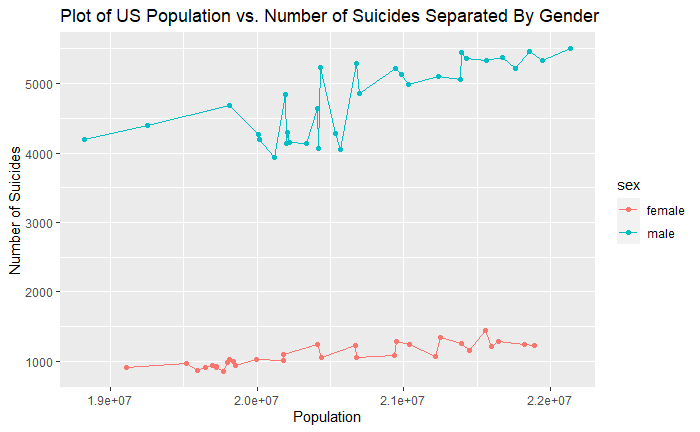
.png)
For the age 25-34 US only population, the correlation between population and total number of suicides was 0.277226 with an R^2 of 0.076 meaning that with these two factors, this only accounts for about 7.6% of the variability in our data though the positive correlation of 0.277 indicates a moderately strong relationship that as population increases, the suicide numbers increase. This relationship is also reflected and applies for both males and females in the scatterplot. This relationship makes sense in that in general, there are going to be more suicides as there are more people around though we cannot say that an increase in population causes the increase number of suicides.
Using a multiple regression model for the age 25-34 US only and running suicide numbers predicted by the other variables we get statistically significant P-values for the variables of male sex as well as population. The variables of year and total_gdp do not have significant p-values in this model. The adjusted R squared value and the R squared value indicating a fairly good fit and since they are both similar at 0.9789 and 0.9774 meaning that this model likely generalizes well given this data. Furthermore, this model suggests that this model accounts for 97% of the variability in our data.
Machine Learning Application
US only data for the 25-34 age population was fed into a K Nearest Neighbors algorithm to predict suicide rate for both males and females and measured by accuracy.
When segmenting our data between country and gender and using the variables of year, country, suicide rate, and GDP for the 25-34 population and using K nearest neighbors, we first get an approximately K value of 11-12 based on the square root of the number of rows in our clean dataset.
sqrt(nrow(usonly25))
usonly25sex <- dummy.code(usonly25$sex)
usonly25suicides <- usonly25$suicides_no
usonly25year <- usonly25$year
usonly25popul <- usonly25$population
usonly25clean <- cbind(usonly25year, usonly25sex, usonly25suicides, usonly25popul)
usonly25clean <- as.data.frame(usonly25clean)
set.seed(1234)
sample <- sample(1:nrow(usonly25clean), 0.8 * nrow(usonly25clean))
knn_train <- usonly25clean[sample,]
knn_test <- usonly25clean[-sample,]
target_cat <- usonly25clean[sample,4]
test_cat <- usonly25clean[-sample,4]
knn <- knn(knn_train, knn_test, cl=target_cat, k=8)
tab <- table(knn, test_cat)
accuracy <- ((sum(diag(tab)))/ (sum(rowSums(tab))))
accuracy
set.seed(12345)
countrymaleml <- countrymale %>% dplyr::select(country, year, suicide_rate, gdp_per_capita)
countryfemaleml <- countryfemale %>% dplyr::select(country, year, suicide_rate, gdp_per_capita)
countrymalemlcountry <- dummy.code(countrymaleml$country)
countrymalemlyear <- countrymaleml$year
countrymalemlsuicide <- countrymaleml$suicide_rate
countrymalemlgdp <- countrymaleml$gdp_per_capita
countrymaleclean <- cbind(countrymalemlcountry, countrymalemlyear, countrymalemlsuicide, countrymalemlgdp)
countrymaleclean <- as.data.frame(countrymaleclean)
countryfemmlcountry <- dummy.code(countryfemaleml$country)
countryfemmlyear <- countryfemaleml$year
countryfemmlsuicide <- countryfemaleml$suicide_rate
countryfemmlgdp <- countryfemaleml$gdp_per_capita
countryfemaleclean <- cbind(countryfemmlcountry, countryfemmlyear, countryfemmlsuicide, countryfemmlgdp)
countryfemaleclean <- as.data.frame(countryfemaleclean)
sqrt(nrow(countrymaleclean))
sample1 <- sample(1:nrow(countrymaleclean), 0.8 * nrow(countrymaleclean))
knn_train1 <- countrymaleclean[sample,]
knn_test1 <- countrymaleclean[-sample,]
target_cat1 <- countrymaleclean[sample, 7]
test_cat1 <- countrymaleclean[-sample, 7]
knn1 <- knn(knn_train1, knn_test1, cl = target_cat1, k = 12)
tab1 <- table(knn1, test_cat1)
accuracy1 <- ((sum(diag(tab1)))/ (sum(rowSums(tab1))))
accuracy1
sample2 <- sample(1:nrow(countryfemaleclean), 0.8 * nrow(countryfemaleclean))
knn_train2 <- countryfemaleclean[sample,]
knn_test2 <- countryfemaleclean[-sample,]
target_cat2 <-countryfemaleclean[sample, 8]
test_cat2 <- countryfemaleclean[-sample, 8]
knn2 <- knn(knn_train2, knn_test2, cl = target_cat2, k = 12)
tab2 <- table(knn2, test_cat2)
accuracy2 <- ((sum(diag(tab2)))/ (sum(rowSums(tab2))))
accuracy2
For the male data, the KNN model is 3.3% accurate at predicting suicide rate given these variables and by country.
For the female data, the KNN model is 1.2% accurate at predicting suicide rate given these variables and by country.
For the US Only Ages 25-34 dataset, I estimated the ideal K to be between 7 and 9. Running the K Nearest Neighbors algorithm using a K of 7, we get a predictive accuracy of 7.69%. This is approximately the same when using a K of 8. Overall, using K Nearest Neighbors to predict the amount of suicides based on year, gender, and population is not accurate.
Conclusions and Future Directions:
These data were collated together using multiple different sources so there could be inherent errors in the data itself and should be interpreted with caution. With my various analyses, there were large residuals however, all had cook’s distance <1 so they likely were not influencing them model. Since this dataset is a summary of suicide rates based on these other factors on a year by year basis, outliers should not necessarily be discarded but examined more closely to see if there was some significant event in that year that could explain the variance.
A note of caution based on South Africa’s data. First, it does not have reporting as early as some of the countries. Germany is the same way. Furthermore, the suicide rates in South Africa are within a very small range between 0 and 1.5 per 100,000 people so the values we get and the changes we see proportionally may not be as large as some of the other countries.
The differences between these graphs present future opportunities for study. For both men and women, why are Germany and France’s suicide rates highest in the 75+ age range category? Are there possibly cultural or country specific circumstances that could correlate with this finding? Why in France, Germany, and the US are 75+ male suicide rates the highest while in the UK it is 35-54 years old?
Why does the female suicide rate at pretty much all age ranges seem to be increasing in the US while male suicide rates appear to have levelled out for most age ranges?
Some of the more interesting information I collected was that male suicide rates for the five countries in question all appear higher than women suicide rates. This could be due to the fact that in general, males are more likely to successfully commit suicide as opposed to females. Even more concerning that out of the five countries, the US male and female suicide rate is the highest. Some of the European’s countries including France and Germany had the highest suicide rate in the highest age ranges. Could this be due to health or economic related factors? For females, the age 35-54 age range seems to have the highest suicide rates for the US and UK while it is 75+ age range for France and Germany. There is significant variability in the South Africa data where it can be hard to make firm conclusions. The dataset for France and Germany also seemed to show a net downward trend in suicide rate as years have passed.
The data here based on these limited variables in this collated dataset appear to violate some of our basic assumptions so generalizing trends or opinions outside of this dataset should be treated with caution. Using K Nearest Neighbors, we saw that based on different variables, our predictive accuracy is unacceptably low in all circumstances.
There are many different factors that play into a country’s suicide rate based on a variety of different factors including socioeconomics, gender, health status, mental health status, etc. Further research would likely require more specific demographic information on population data.
For full code of the project, please refer to my GitHub repository under Data Science Statistics.